I got a bit stuck with the work I was planning for today, so I wrote something else to regain motivation: a fractal! Rendering takes a while, being fully interpreted and lacking multiplication, and even without the “right-shift” operation you badly need for this. All those must be mimicked with slow high-level code using just addition and subtraction.
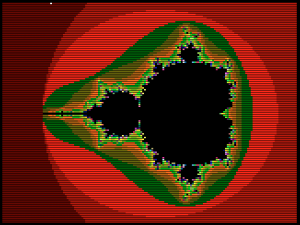
It should be easy to speed the whole thing up a lot just by adding a right-shift assembly function. Next time… GCL source code:
{-----------------------------------------------------------------------+
| |
| Mandelbrot fractal |
| |
+-----------------------------------------------------------------------}
gcl0x
{
Plot the Mandelbrot set
- 160x120 pixels and 64 colors
- Faithful translation of mandelbrot.c pre-study
- Use 16-bit vCPU math as 7-bit fixed point arithmetic (1.00 -> 128)
- Implement multiplication in interpreter
- Implement shift-right in interpreter as well
- A bit slow (8242.655 seconds)
XXX At the end change all to grey tones and redo
XXX Redo at different sections
XXX Tone for every pixel value
}
{-----------------------------------------------------------------------+
| RAM page 3 |
+-----------------------------------------------------------------------}
$0300:
{ Pretty accurate multiply-shift ((A*B)>>7), but it can be off by one }
[def
push
{Extract sign and absolute values}
0 sign= C=
{0}A- [if>0 A= 1 sign=]
0 B- [if>0 B= sign 1^ sign=]
{Multiply}
7 shift= {Pending shift}
$200
[do
bit=
-$4000 C+ [if<0 C C+ C= else {Shift prematurely in an attempt to avoid overflow} B ShiftRight! B= shift 1- shift=] {Add partial product} A bit- [if>=0
A=
C B+ C=]
bit ShiftRight! if<>0loop]
{Shift}
[do
C ShiftRight! C=
shift 1- shift= if>0loop]
{Apply sign to return value}
sign [if<>0 0 C- else C]
pop ret
] MulShift7=
{ Calculate color for (X0,Y0) }
[def
push
0 X= XX= Y= YY= i=
[do
i 1+ i= 64^ if<>0 {Break after 64 iterations}
{Mandelbrot function: z' := z^2 + c}
X A= Y Y+ B= MulShift7! Y0+ Y= {Y = 2*X*Y + Y0}
XX YY- X0+ X= {X = X^2 - Y^2 + X0}
{Calculate squares}
{X}A= B= MulShift7! XX=
Y A= B= MulShift7! YY=
-$200 XX+ YY+ if<0loop] {Also break when X^2 + Y^2 >= 4}
i
pop ret
] CalcPixel=
{-----------------------------------------------------------------------+
|}\vLR>++ ret{ RAM page 4 |
+-----------------------------------------------------------------------}
$0400:
[def
push
$7ff p= {Start of video (minus 1 to compensate for 1st step)}
-323 X0= 3 DX= 161 Width= {Horizontal parameters}
-180 Y0= 0 DY= 120 Height= {Vertical parameters}
[do
{Length of next segment, either horizontal or vertical}
DX [if<>0 Width 1- Width= else Height 1- Height=] if>0
[do
len=
{Step in the fractal plane}
X0 DX+ X0=
Y0 DY+ Y0=
{Matching step in video frame}
DX [if<0 p 1- p=] DX [if>0 p 1+ p=]
DY [if<0 -$100 p+ p=] DY [if>0 $100 p+ p=]
63 p. {White while busy here}
{First check if we are inside one of the main bulbs for
a quick bailout (Wikipedia)
(x+1)^ + y^2 < 1/16}
Y0 A= B= MulShift7! YY=
X0 128+ A= B= MulShift7! YY+ 8- [if<0 0
else
{q*(q + x - 1/4) < 1/4*y^2, where q = (x - 1/4)^2 + y^2}
X0 32- A= B= MulShift7! YY+ {q}
A= X0+ 32- B= MulShift7! tmp=
tmp+ tmp= tmp+ tmp= {*4} YY- [if<0 0 else {Otherwise run the escape algorithm} CalcPixel! ]] p. {Plot pixel} len 1- if>0loop]
DY tmp= DX DY= 0 tmp- DX= {Turn right}
loop]
pop ret
] CalcSet=
{-----------------------------------------------------------------------+
|}\vLR>++ ret{ RAM page 5 |
+-----------------------------------------------------------------------}
$0500:
{ Stupid shift-right function }
{ XXX Better make a SYS extension for this }
[def
a= 0 b=
$8000 a+ [if>=0 a= $4000 b+ b=]
$c000 a+ [if>=0 a= $2000 b+ b=]
$e000 a+ [if>=0 a= $1000 b+ b=]
$f000 a+ [if>=0 a= $0800 b+ b=]
$f800 a+ [if>=0 a= $0400 b+ b=]
$fc00 a+ [if>=0 a= $0200 b+ b=]
$fe00 a+ [if>=0 a= $0100 b+ b=]
$ff00 a+ [if>=0 a= $0080 b+ b=]
$ff80 a+ [if>=0 a= $0040 b+ b=]
$ffc0 a+ [if>=0 a= $0020 b+ b=]
$ffe0 a+ [if>=0 a= $0010 b+ b=]
$fff0 a+ [if>=0 a= $0008 b+ b=]
$fff8 a+ [if>=0 a= $0004 b+ b=]
$fffc a+ [if>=0 a= $0002 b+ b=]
a 2& [if<>0 b<++ ] b ret ] ShiftRight= {-----------------------------------------------------------------------+ |}\vLR>++ ret{ RAM page 6 |
+-----------------------------------------------------------------------}
$0600:
{ Main }
[do
CalcSet!
60 \soundTimer. {For debugging}
loop]
{-----------------------------------------------------------------------+
| End |
+-----------------------------------------------------------------------}
– Marcel

